郭 爽, 范江华
(广西师范大学 数学与统计学院, 广西 桂林 541006)
函数极小值问题解的存在性是最优化理论研究的一个基本问题, 解集的有界性在数值计算的算法设计中有重要应用. 关于凸函数极小值问题解的存在性与解集的有界性研究目前已有较完善的结果[1-2]. 凸性在最优化理论、 数理经济和工程技术等领域应用广泛. 而在实际问题中, 很多函数不具有凸性, 所以研究各类广义凸函数及其应用具有重要意义. Mangasarian[3]引进了拟凸和伪凸函数的概念, 并研究了其性质; Flores-Bazn等[4]在有限维空间中研究了拟凸函数的极大值和极小值问题, 并引入了q-渐近函数的概念; Baiocchi等[5]研究了非凸非强制性泛函的极小值问题; Penot[6]利用拟凸函数的几种次微分给出了拟凸函数极小值存在解的充分条件; Iusem等[7]利用渐近分析研究了自反Banach空间中的拟凸函数极小值问题解集的非空有界性; 文献[8]在有限维空间中利用拟凸函数的1阶和2阶渐近分析研究了拟凸函数的极小值问题.
本文考虑拟凸函数极小值问题解集的非空有界性. 利用渐近分析讨论自反Banach空间中的拟凸优化问题. 首先给出非空闭凸集上拟凸函数的q-渐近函数的定义, 然后利用非空闭凸集上拟凸函数的q-渐近函数, 给出拟凸函数极小值问题解集存在性的等价刻画. 本文结果将经典的凸函数极小值问题解集的非空有界性结果推广到拟凸函数上, 并给出平衡问题解集非空有界的一个充分条件.
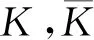
给定任一函数f:V→∪{+∞}, 其定义域为
domf={x∈V:f(x)<+∞}.
记f的上方图形为epif∶={(x,t)∈V×:f(x)≤t}; 记f的水平集为Sλ(f)∶={x∈V:f(x)≤λ}.设f表示f在K上所有极小点构成的集合, 定义为
设K是V中的弱闭集, 记K∞为K的渐近锥, 定义为
K∞∶={u∈V: ∃tk↓0, ∃xk∈K,tkxk⇀u}.
特别地, (Ø)∞=Ø.若K是闭凸集, 则根据文献[7]有
K∞∶={u∈V:x0+λu∈K, ∀λ>0}, ∀x0∈K.
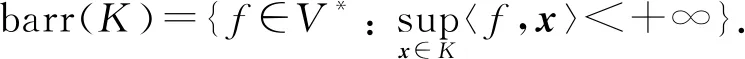
给定任一函数f:V→∪{+∞}, 记∪{±∞}为f的渐近函数, 定义为epif∞∶=(epif)∞.由文献[4]有
若f为凸下半连续函数, 则epif为闭凸集, 且对所有的x0∈domf, 有
定义1[2]若函数f:V→∪{+∞}的定义域domf是一个凸集, 且对任意的x,y∈V,t∈[0,1], 有
f(tx+(1-t)y)≤max{f(x),f(y)},
则f称为拟凸函数.
f的凸性和拟凸性可分别用f的上方图和水平集进行表征,f为凸函数当且仅当epif为凸集;f为拟凸函数当且仅当对任意的λ∈,Sλf为凸集.
定义2[2]设f:V→∪{+∞}是真函数.
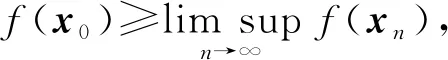
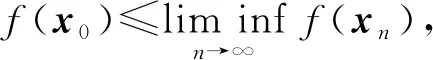
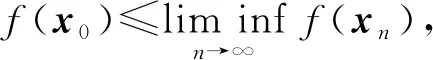
由定义2易知,f在V上是上半连续函数当且仅当(-f)在V上是下半连续函数; 弱下半连续函数必为下半连续函数; 自反Banach空间中凸下半连续函数为弱下半连续函数.
定义3[1]设f:V→∪{+∞}是真函数, 定义f的q-渐近函数为
令K=epif, 易见
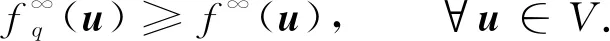
(1)
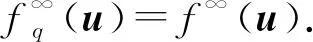
定义4设f:V→∪{+∞}是真函数,K⊂domf为闭凸集, 定义f在K上的q-渐近函数为

下面利用闭凸集上拟凸函数的q-渐近函数讨论非强制拟凸极小值问题解集的非空有界性.设f:V→∪{+∞}为真函数,K⊂domf为闭凸集, 考虑其极小值问题
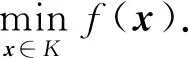
(2)
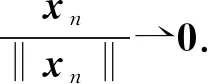
引理2[10]设U为X中的序列弱紧集,f是U上的下半弱连续泛函, 则f在U上能达到极小值.
下面给出本文的主要结果----闭凸集上弱下半连续拟凸函数最小化问题解集的非空有界性.
定理1设K为一个自反Banach空间V中的非空闭凸子集, 且int(barrK)≠Ø, 设f:V→为弱下半连续拟凸函数, 且K⊂domf, 则下列结论等价:
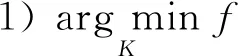
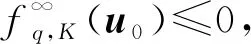
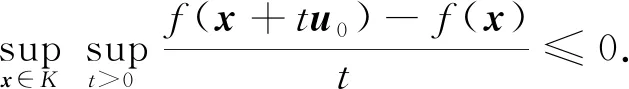
(3)
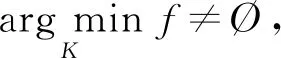
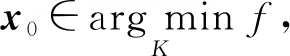
2)⟹1).对每个自然数k, 记集合Kk∶={x∈K: ‖x‖≤k}.显然, 存在k1>0, 使得当k≥k1时,Kk为非空有界闭凸集, 故Kk为序列弱紧集.因为f:V→为弱下半连续泛函, 所以由引理2可知,f在Kk上取得最小值, 从而f为非空集合, 又因为Kk为有界集, 故f为非空有界集合.
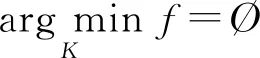
(i) ‖xk‖=k;
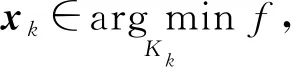
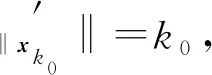
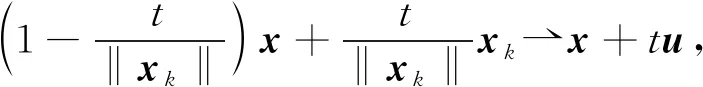
(4)
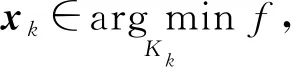
即对任意的x∈K和t>0, 有
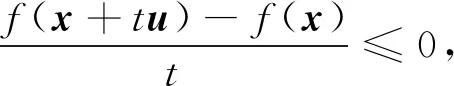
(6)
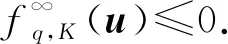
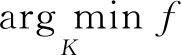
综上可知, 条件1)与条件2)等价.
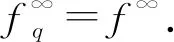
推论1[1]设K为n的非空闭凸子集,f:n→为下半连续凸函数, 且K⊂domf, 则下列结论等价:
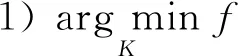
2) 对任意的u∈K∞{0},f∞(u)>0.
下面给出文献[7]中定理3.2, 其假设条件如下:
(H1) 设(V,‖·‖)是Banach空间,σ是V上比范数拓扑弱的拓扑, 且(V,σ)是Hausdorff向量空间, 其闭单位球是序列σ-紧集, 若h:V→∪{+∞}为序列σ-下半连续函数,tk→+∞,vk按σ-收敛到v, 且h(tkvk)有上界, 则‖vk-v‖→0.
定理2[7]设(V,‖·‖)为一个自反Banach空间, 且h:V→∪{+∞}为真弱下半连续的拟凸函数.若条件(H1)成立, 则是非空弱紧集当且仅当下列条件成立:
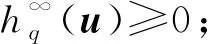
注1定理1与定理2相比, 定理1给出了闭凸集上拟凸函数极小值问题解集的非空有界性, 定理2给出了定义域上拟凸函数极小值问题解集的非空有界性.因为弱下半连续函数的极小值点集为弱闭集, 故弱下半连续函数的最小值点集为非空有界集当且仅当它为弱紧集.下面给出满足定理1 条件, 但不满足条件(H1)的实例.
例1设V=l2,K∶={x=(η1,η2,…,ηn,…)∈l2: 2η1≥‖x‖}, 则由文献[9]可知, int(barr(K))≠Ø.设
显然,K⊂domf.首先说明f:V→为拟凸函数.任取t∈(0,1).对x,y∈K, 下列结论成立:
1) 若x或y中有一个范数大于1, 则显然有
f(tx+(1-t)y)≤1≤max{f(x),f(y)};
2) 若‖x‖≤1, ‖y‖≤1, 则
‖tx-(1-t)y‖≤1,
若x,y中有一个不属于K, 则显然有f(tx+(1-t)y)≤max{f(x),f(y)}.由范数函数‖·‖的弱下半连续性可知,f:V→为弱下半连续函数.
对任一u∈K∞{0}, 取t0>0,t1>0, 使得‖t0u‖<1, ‖(t0+t1)u‖>1, 因为0∈K, 故t0u∈K,t0u+t1u∈K, 且
从而f:K→满足定理1的条件.令vn=e1+en,λn=n, 则f(λnvn)=1,vn⇀e1.注意到vne1, 因此,f不满足条件(H1).
文献[4]在有限维空间中讨论了拟凸函数极小值解集的非空有界性, 得到如下结果.
定理3[4]令f:n→∪{+∞}为下半连续的拟凸函数, 且domf≠Ø, 则下列条件等价:
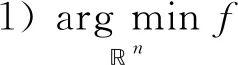
2)Rq={0};
定理4设K为一个自反Banach空间(V,‖·‖)中的非空闭凸子集, 且int(barrK)≠Ø, 设f:V→为拟凸弱下半连续函数, 且K⊂domf, 则下列条件等价:
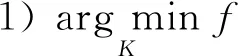
2)Rq,K={0};
因此, 在1)~3)任意一种条件下, 均有
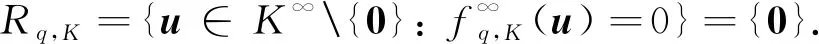
(7)
证明:
由定理1可知1)⟺3).2)⟺3)显然.因为
故在1)~3)任意一种条件下均有式(7).
注2定理4将定理3的结果从有限维空间推广到了无限维自反Banach空间.
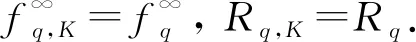
推论2设K为一个自反Banach空间(V,‖·‖)中的非空闭凸子集, 且int(barrK)≠Ø, 设f:V→为拟凸弱下半连续函数, 且domf=K, 则下列条件等价:
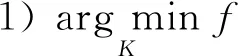
2)Rq={0};
注3当domf=K时, 推论2在int(barrK)≠Ø条件下得到的结论强于在条件(H1)下得到的结论.例1满足推论2的条件.
下面给出平衡问题解集非空有界的一个充分条件.设K⊂V是非空闭凸集,φ:K×K→, 考虑如下平衡问题: 存在使得

(8)

函数φ满足下列条件:
(i) 对任意的x∈K,φ(x,x)=0;
(ii) 对所有的x∈K,φ(x,·)是弱下半连续的拟凸函数;
(iii) 对每个x∈K及每个y∈K,φ为伪单调函数, 即若φ(x,y)≥0, 则有φ(y,x)≤0;
(iv) 对所有的y∈K,φ(·,y)是弱上半连续函数.
下面引入二元函数φ的q-渐近函数的概念.
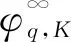
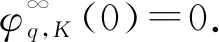
引理3[11]设K⊂V为有界闭凸集,φ:V×V→满足条件(i)~(iv), 且K×K⊂domφ.则平衡问题(8)的解集S(K,φ)为非空集合.
定理5设K⊂V是非空无界闭凸集且int(barrK)≠Ø,φ:V×V→满足条件(i)~(iv), 且K×K⊂domφ.若对任一u∈K∞{0}, 均有则平衡问题(8)的解集S(K,φ)为非空有界集.
证明:
对任一n∈, 考虑如下问题: 存在使得

(9)
由于Kn是弱紧集, 由引理2知问题(9)的解集为非空集, 记其中一个解为xn, 则对任意的y∈Kn, 有φ(xn,y)≥0.
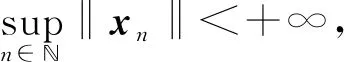
φ(xn,y)≥0, ∀n≥n0.
从而有
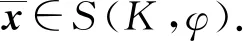
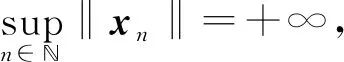
φ(xn,y)≥0(∀n≥n0) ⟹φ(y,xn)≤0(∀n≥n0).
(10)
显然, 对任意的t>0, 当n充分大时, 有
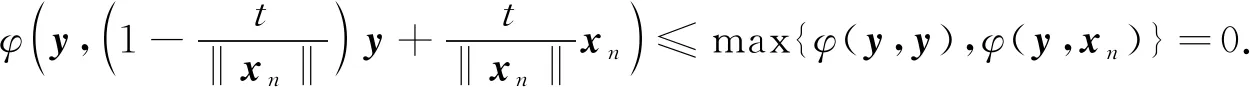
(11)
又因为φ(y,·)是弱下半连续函数, 故有
φ(y,y+tu)≤0, ∀y∈K, ∀t>0.
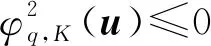
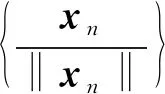
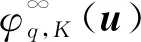
例2设X=n,K={x=(x1,0,…,0),x1≥0},φ:K×K→,则K∞=K, 对任一u∈K∞{0}, 当u1>0,t1>0时, 均有
故φ,K满足定理5的条件.
猜你喜欢极小值等价定理J. Liouville定理中等数学(2022年6期)2022-08-29等价转化新高考·高三数学(2022年3期)2022-04-28一道抽象函数题的解法思考与改编*中学数学研究(江西)(2020年5期)2020-07-03构造可导解析函数常见类型例析*中学数学研究(江西)(2019年11期)2019-12-31A Study on English listening status of students in vocational school校园英语·上旬(2019年6期)2019-10-09极小值原理及应用科技风(2018年19期)2018-05-14n次自然数幂和的一个等价无穷大中文信息(2017年12期)2018-01-27“三共定理”及其应用(上)中学生数理化·七年级数学人教版(2017年6期)2017-11-09基于庞特里亚金极小值原理的多运载体有限时间编队控制自动化学报(2017年1期)2017-03-11收敛的非线性迭代数列xn+1=g(xn)的等价数列中央民族大学学报(自然科学版)(2015年2期)2015-06-09