孙海莹,扎其劳,2
(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022;
2.内蒙古自治区应用数学中心,内蒙古 呼和浩特 010022)
非线性科学的研究对象是混沌、孤子和分形,其中,孤子是非线性动态系统中色散与非线性平衡的结果,是一类非线性波。作为一种典型的非线性现象,非线性波经常在非线性光学、电磁学、等离子体物理学、凝聚态物理学和生物学中出现。由于求解非线性演化方程的难度很大,所以对不同方程采用的求解方法各不相同,研究者需要寻找更新、更有效的方法来获得显式解。因此,寻找非线性演化方程的精确解是一项重要而有意义的工作。研究者在孤立子与可积系统理论中建立了一些求解非线性演化方程的精确解的有效方法,例如反散射方法[1]、李群法[2]、Jacobi 椭圆函数展开法[3-4]、Hirota 双线性法[5-6]、达布变换法[7-9]、贝克隆变换[10],辅助方程法等[11]。
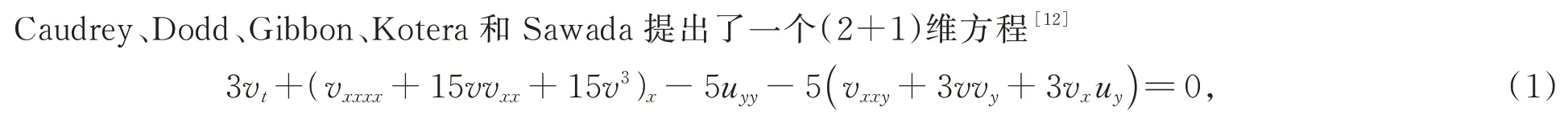
其中u,v是关于变量x,y,t的函数。通过v=ux的变换,方程(1)变成(2+1)维CDGKS 方程[12]
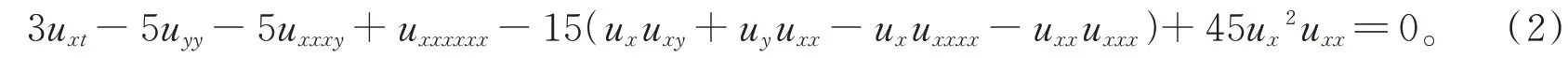
方程(2)作为Kadomtsev-Petviashvil(iKP)方程的高阶推广形式[13],源于可积系统的无限对称性,它能很好地描述非线性色散物理现象,广泛应用于许多物理分支。如二维量子引力规范场理论和共形场理论[14]。关于(2+1)维CDGKS 方程现在已有较多研究工作,例如Konopelchenko 和Dubovsky[13]提出的五阶非线性演化方程引起了众多学者的关注,他们通过考虑两个给定的算子的交换性条件,给出了(2+1)维CDGKS方程的相容性条件。Sidra Saleem 和Malik Zawwar Hussain[15]指出传统的五阶KdV 方程可以变成(1+1)维CDGKS 方程。通过取适当的系数值,方程(1)可以看作是传统的五阶KdV 方程向(2+1)维的扩展,这类似KdV 方程和KP 方程的关系。到目前为止方程(2)的许多不同类型的精确解,如周期解[16],怪波解[17],lump解[18]等已经得到广泛研究,但关于(2+1)维CDGKS 方程的混合波解的研究还很少。所以本文基于Hirota双线性方程和长波极限法,通过构造合适的辅助函数推导出了CDGKS 方程N-kink 解、L-呼吸子解和Klump 解的混合波解。
为了获得方程(2)的显式解,在变换

下,其中f是关于变量x,y,t的函数,方程(2)可转化为双线性形式
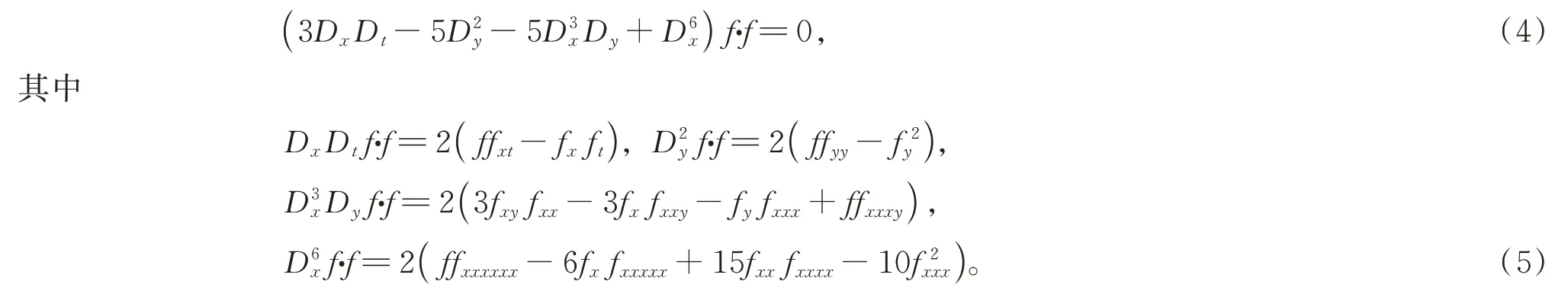
变换(3)表明u=u(x,y,t)是方程(2)的解当且仅当f=f(x,y,t)是双线性方程(4)的解。
1.1 N-kink 解
首先假设u具有如下形式

将方程(6)带入方程(2)的线性部分,得到色散关系的表达式为
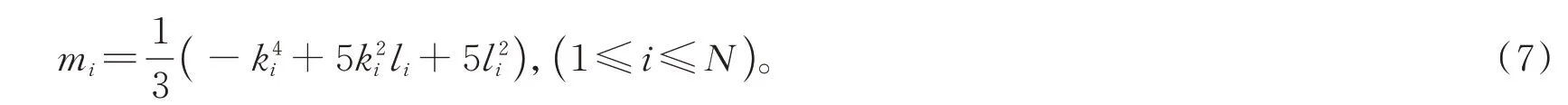
选择辅助函数[19]

其中ki,li是常数,μi=0,1(1 ≤i≤N),并且有

将方程(10)—(13)带入方程(3)中并选取适当的参数,可以得到方程(2)的1-、2-、3-、4-kink 解。
1.2 L-呼吸子解
借助2L-kink 解的辅助函数,并取参数两两为复共轭,可以得到方程(2)的L-呼吸子解。但由于解的非奇异性,因此必须保证参数ki,li,eAij满足以下要求[20]
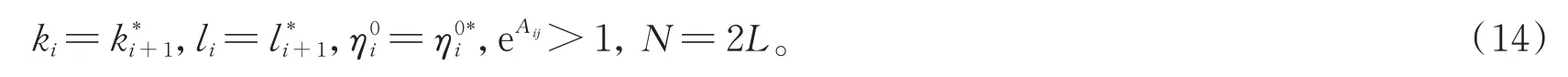
因此,在得到2L-kink 解的前提下,就得到了L-呼吸子解。本文只给出1-呼吸子解和2-呼吸子解这两种情况。当L=1 时,将方程(11)带入方程(3)可得到

令k1=-1+2i,k2=-1-2i,l1=-2+i,l2=-2-i,t=0,会获得方程(2)的1-呼吸子解,如图1(a)所示。
当L=2 时,重复获得1-呼吸子解的方法,将方程(13)带入方程(3)可得


图1 方程(2)的1-呼吸子解和2-呼吸子解Fig.1 One-breather and two-breather solution of equation(2)
1.3 K-lump 解
使用长波极限法获得方程(2)的lump 解。由于篇幅有限,因此在本文中只给出1-lump 和2-lump 解。令,然后辅助函数fN变成[21-22]

当N=2 时,令方程(17)中k1→0,k2→0,收集k1k2的系数后辅助方程f2变成

当N=4 时,令方程(17)中ki→0(i=1,2,3,4),收集k1、k2、k3、k4的系数后辅助方程f4变成

将方程(19)带入方程(3),得到方程(2)的2-lump 解,如图2(b)所示。
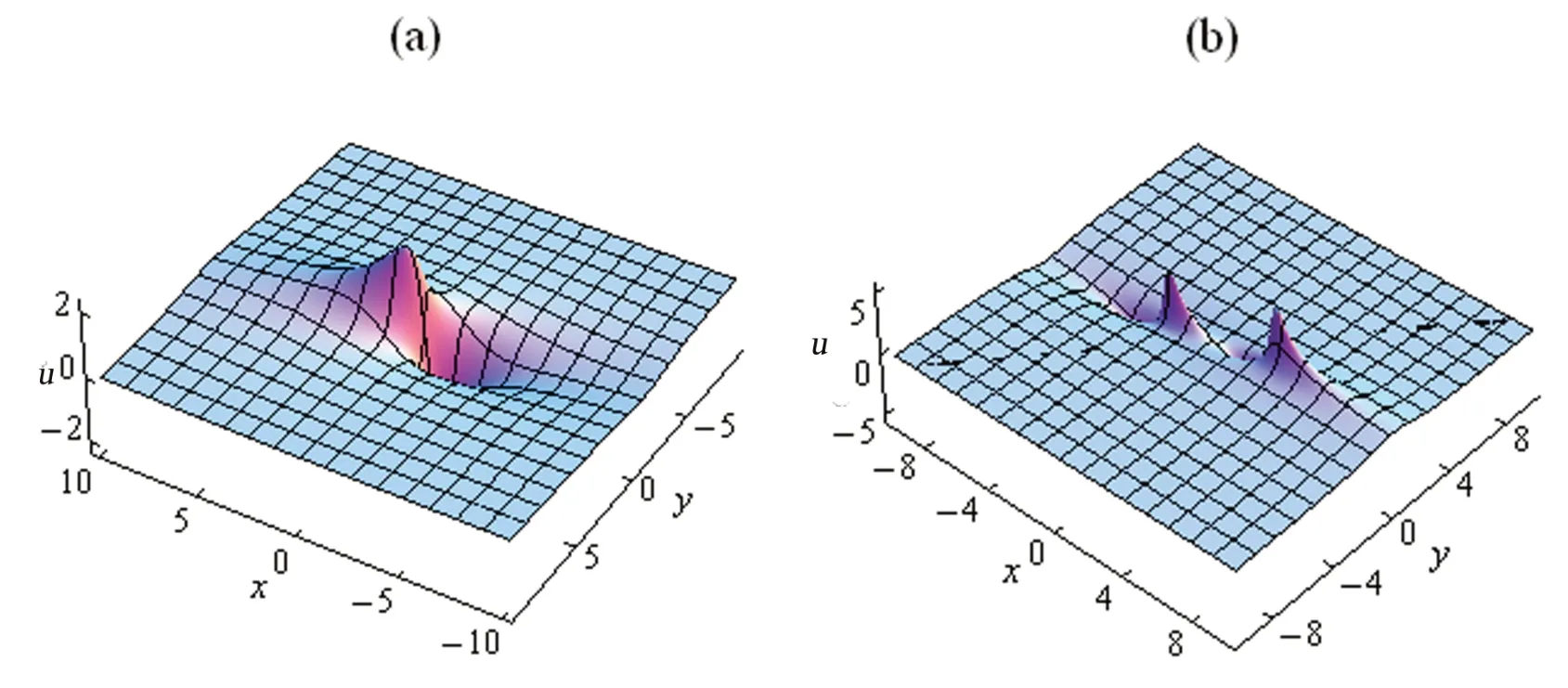
图2 方程(2)的1-lump 解和2-lump 解Fig.2 The first-order and the second-order lump solution of equation(2)
讨论方程(2)的四种混合波解。通过选择合适的参数值,可以得到N-kink 解和L-呼吸子的混合波解。将长波极限法应用于方程(17)得到新的辅助函数,可以求出由lump 解和其他两种解组成的混合波解。
2.1 Kink 和呼吸子的混合波解
当N=4 时,将方程(13)代入方程(3),令-1,k4=2,t=0,可以构造出2-kink 和1-呼吸子的混合波解,如图3(a)。
当方程(8)中N=5 时,将表达式带入方程(3)。通过选取合适的参数,可以得到两组混合解,分别是3-kink和1-呼吸子的混合波解、以及1-kink 和2-呼吸子的混合波解,如图3(b)和3(c)。

图3 方程(2)的kink 和呼吸子的混合波解Fig.3 Mixed solution of kink and breather of equation(2)
2.2 Kink 和lump 的混合解
为了构造由1-kink 和1-lump 组成的混合解,需要令方程(12)中的且k1→0,k2→0。收集k1k2的系数后辅助方程f3取为
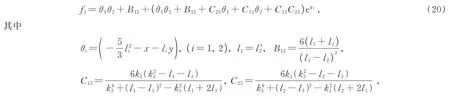

将方程(20)带入方程(3)中,可以得到1-kink 和1-lump 的混合波解

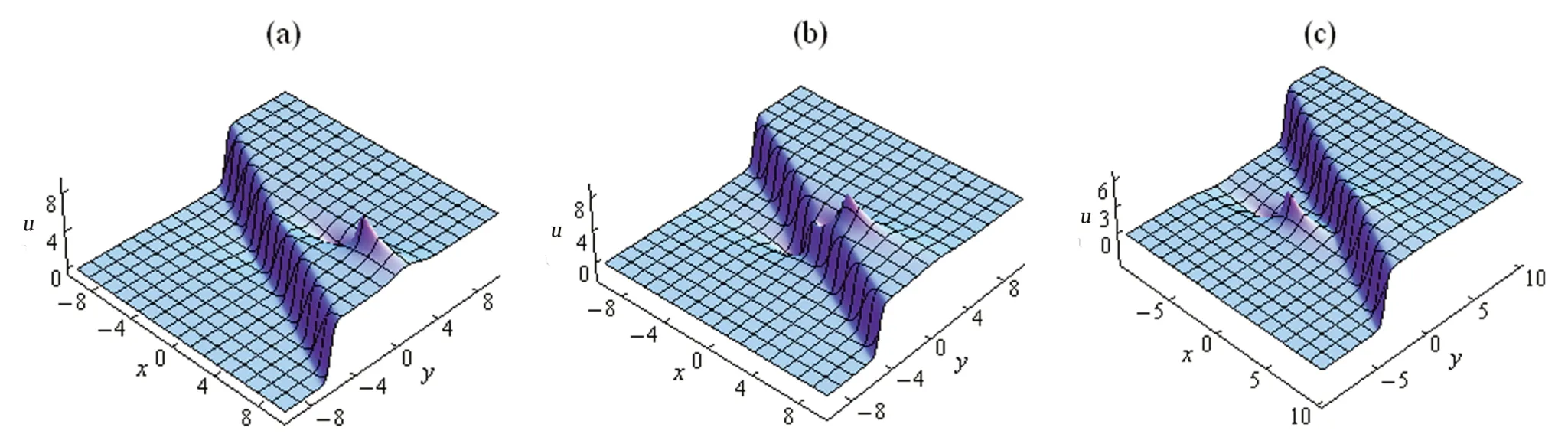
图4 方程(2)的1-kink 和1-lump 的混合波解Fig.4 Mixed solution of one-kink and the first-order lump of equation(2)
当N=4 时,令方程(13)中的且k1→0,k2→0,可以获得2-kink 和1-lump 的混合波解。重复上述步骤,即收集k1k2的系数后辅助方程f4化成
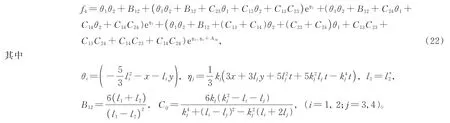
将方程(22)带入方程(3),可以得到2-kink 和1-lump 的混合波解u=2(lnf4)x。选取参数-1-2i,l3=2,k3=3,l4=-2,k4=2,t=-1/2,0,1/2,利用Mathematica 软件画图展示了2-kink 和1-lump的相互作用。在图5(a)中,2-kink 和1-lump 解分离,在图5(b)中它们发生碰撞,然后2-kink 和1-lump 保持形状速度恒定沿着y轴正向移动,在图5(c)中可以看出二者随着时间的增加仅仅改变了位置。

图5 方程(2)的2-kink 和1-lump 的混合解Fig.5 Mixed solution of two-kink and the first-order lump of equation(2)
当N=5 时,令方程(8)中的且k1→0,k2→0,此时构造3-kink 和1-lump的混合解的辅助函数变成
其中


图6 方程(2)的3-kink 和1-lump 的混合波解Fig.6 Mixed solution of three-kink and the first-order lump of equation(2)
如果要构造1-kink 和2-lump 的混合波解的辅助函数,则令方程(8)中N=5 时的且ki→0(i=1,2,3,4),此时辅助函数f5变成
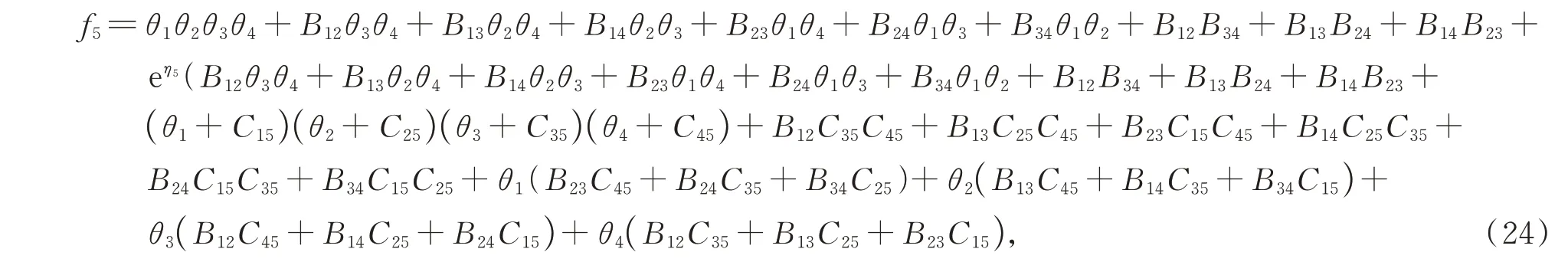
其中θi,Bij,Cr5(i,j,r=1,2,3,4)的表达形式同方程(23)的保持一致。将方程(24)带入方程(3),并取参数-2,k3=-2,l4=2,k4=1,l5=-1,k5=-2,t=-1/2,0,1/2,可以得到1-kink 和2-lump 的混合波解。如图7(a)-(c)。

图7 方程(2)的1-kink 和2-lump 的混合波解Fig.7 Mixed solution of one-kink and the second-order lump of equation(2)
2.3 呼吸子和lump 的混合波解
基于已经得到的2-kink 和1-lump 的混合波解,若要获得呼吸子和lump 的混合波解,则需要为已经得到的辅助方程(22)添加参数约束条件
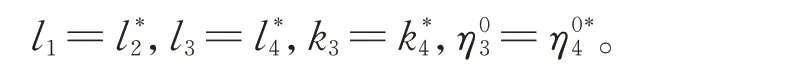

图8 方程(2)的1 呼吸子和1-lump 的混合波解Fig.8 Mixed solution of one-breather and the first-order lump of equation(2)
2.4 方程的kink-呼吸子-lump 的混合波解
当N=5 时,通过方程(23)的辅助函数,得到了1-kink、1-呼吸子和1-lump 的混合解[23-24]。在图9 中描述了三者在时间变化下的演化过程,可以看到随着时间的推移,1-lump 是沿x轴的正方向移动。当t=-1/5 时,lump 在呼吸子的左边。当t=0 时,1-kink、1-呼吸子和1-lump 发生弹性碰撞。当t=1/5 时,lump 运动到呼吸子的右边。
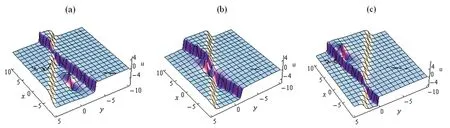
图9 方程(2)的1-kink、1 呼吸子和1-lump 的混合解Fig.9 Mixed solution of one-kink,one-breather and the first-order lump of equation(2)
本文主要研究了(2+1)维CDGKS 方程的混合波解。首先基于Hirota 双线性方程和长波极限方法,得到了方程的N-kink、L-呼吸子和K-lump 解。接着利用不同的辅助函数,讨论了四类混合波解,分别是N-kink和L-呼吸子混合波解、N-kink 和K-lump 混合波解、L-呼吸子和K-lump 混合波解、1-kink、1-呼吸子和1-lump的混合波解。通过对参数取特殊值,并借助数学软件绘图,从图中可以看出混合解的动态行为。已知求解精确解的常用方法有Hirota 双线性法和长波极限法,本文将这两种方法很好地结合起来。结果证明,发现相互作用波之间的碰撞是弹性碰撞,得到的解可以理解流体力学中非线性波的传播过程,丰富非线性现象的动力学行为。研究非线性发展方程的相互作用解具有重要的数学和物理意义,本文采用的方法具有一定的普适性,为未来对高维非线性发展方程的高阶混合波解的研究提供借鉴。
猜你喜欢 长波辅助方程 方程的再认识中学生数理化·七年级数学人教版(2022年5期)2022-06-05小议灵活构造辅助函数河北理科教学研究(2021年3期)2022-01-18方程(组)的由来中学生数理化·七年级数学人教版(2021年5期)2021-11-22倒开水辅助装置发明与创新(2021年39期)2021-11-05广义对称正则长波方程的孤波解和周期波解及它们与Hamilton能量的关系数学物理学报(2021年3期)2021-07-19圆的方程新世纪智能(数学备考)(2020年12期)2020-03-29基于大数据分析的易混淆车辅助识别系统设计与实现中国交通信息化(2019年10期)2019-11-16提高车辆响应的转向辅助控制系统汽车文摘(2015年11期)2015-12-02基于构架点头角速度的轨道垂向长波不平顺在线检测中国铁道科学(2015年4期)2015-06-21扫描型长波红外连续变焦光学系统中国光学(2015年1期)2015-06-06