方珍洁,龙宪军
(重庆工商大学数学与统计学院 重庆 400067)












为了体现本文讨论的算法的数值效果,本节通过例子将算法3.1与文献[16]中的算法4(记为RITEM算法),文献[14]中的算法3.5(记为ITEM算法)和文献[15]中的算法1(记为MTEM算法)进行比较.所有代码均在MATLAB R2019b和Windows10系统下运行,计算机基本参数为Intel(R)Core(TM)i5-10210U CPU@1.60GHz 2.11GHz和16GB内存.
例 4.1设算子F:Rm→Rm(m=50,100)满足F(x)=Mx+q,其中q∈Rm,同时M=NNT+S+D,其中N∈Rm×m,S∈Rm×m斜对称矩阵,D∈Rm×m对角元素非负的对角矩,可行集C=R+m.各参数选取如下:

初始点x0=(1,1,···,1)T∈Rm,终止条件为Dn=∥xn+1−xn∥,测试结果见图1,图2和表1.通过图1,图2和表1可以发现,算法3.1比文献[16]中RITEM算法,文献[14]中ITEM算法和文献[15]中MTEM算法收敛效果更好.

图1 固定误差比较图

图2 固定迭代步数比较图

表1 例4.1算法结果对比表
例4.2假设H=l2,令

定义算子F:C→H,存在α>0,满足

显然,F在H上是伪单调的且一致连续的,在C上是序列弱连续的.令α=0.5,可行集

各参数选取如下:

初始点x0=[0,1]m,用∥xn∥来估算第n步迭代误差值.由于F既不是单调的,也不是Lipschitz连续的,故文献[16]中RITEM算法和文献[14]中ITEM算法不适用于本例.测试结果见图3,图4和表2.通过图3,图4和表2可以发现,算法3.1比文献[15]中MTEM算法迭代次数少,收敛速度更快.
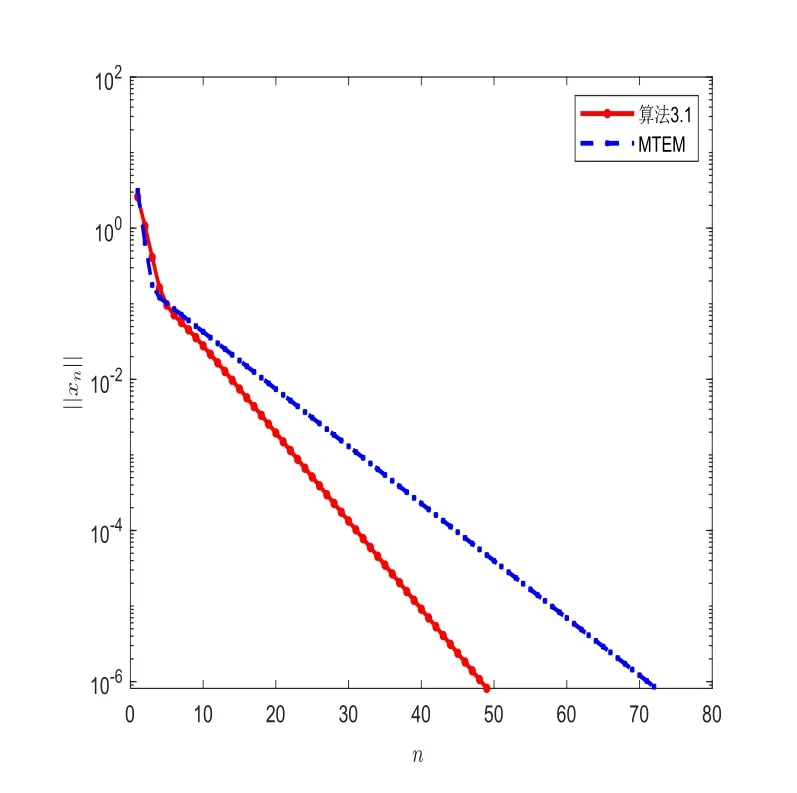
图3 固定误差比较图

图4 固定迭代步数比较图

表2 例4.2算法结果对比表
从数值实验的结果来看,得出结论:
(i)由图 2可得,在相同的迭代步数下,算法 3.1比 RITEM 算法,MTEM 算法和ITEM算法的误差Dn更小,更接近于变分不等式的解.
(ii)由图 1和表 1可得,在达到相同的误差Dn时,算法 3.1比 RITEM 算法,MTEM算法和ITEM算法运行的时间更短,迭代步数更少.
(iii)由例4.2可得,算法3.1和MTEM算法比ITEM算法和RITEM算法适用范围更广.
(iv)由图4可得,在相同的迭代步数下,算法3.1比MTEM算法得到的误差更小.
(v)由图3和表2可得,在达到相同误差时,算法3.1比MTEM算法迭代步数更少,运行时间更短.
(vi)算法3.1,RITEM算法,ITEM算法和MTEM算法均收敛于变分不等式的解,算法3.1优于RITEM算法,ITEM算法和MTEM算法.
猜你喜欢 变分对角步数 求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法数学物理学报(2022年5期)2022-10-09楚国的探索之旅奇妙博物馆(2021年4期)2021-05-04微信运动步数识人指南小演奏家(2018年9期)2018-12-06会变形的忍者飞镖数学大王·低年级(2018年4期)2018-05-07自反巴拿赫空间中方向扰动的广义混合变分不等式的可解性Acta Mathematica Scientia(English Series)(2018年6期)2018-03-01国人运动偏爱健走党的生活(黑龙江)(2017年10期)2017-11-09基于变分水平集方法的数字图像分割研究中国市场(2016年45期)2016-05-17对角占优矩阵的判定条件科技视界(2014年26期)2014-12-25具有(H,η)单调算子的广义非线性变分包含财经界·下旬刊(2009年5期)2009-12-30折大象小朋友·快乐手工(2009年1期)2009-02-07