Rashid Jan,Salah Boulaaras and Syed Azhar Ali Shah
1 Department of Mathematics,University of Swabi,Swabi 23430,KPK,Pakistan
2 Department of Mathematics,College of Sciences and Arts,ArRass,Qassim University,Saudi Arabia
Abstract It is undeniable that HIV infection has been a censorious public health concern over the past four decades.It is reported that HIV is the main reason for AIDs which has decimated the global population of humans and imposed a significant economic burden on affected areas.Hence,it is significant to study the transmission of HIV viruses in the body of a human host.In this study,we use a fractional framework to organise the intricate interactions of CD4+ T-cells and HIV viruses in order to investigate HIV infection with control interventions.We apply the operators of Caputo and Atangana–Baleanu to interrogate the transmission phenomena of HIV viruses.For the analysis of our system,we present the basic concepts of the fractional operators.Numerical schemes are provided to show the solution pathways of the system with the variation of input parameters.Furthermore,the findings emphasise the chaotic and dynamical behaviour of HIV.We run several simulations to visualise the influence of input factors and quantitatively illustrated the dynamics of HIV.Chaos and oscillatory behaviour are intimately linked,and this is owing to the system’s nonlinearity.Furthermore,our findings indicate the most important factors for infection control and prevention.
Keywords:fractional-calculus,HIV infection,dynamics of HIV,numerical method,time series analysis
It is reported that the infection of HIV weakens the immune system of a human host and damages bodily systems such as the heart,kidneys and brain,ultimately leading to death.Unfortunately,there is currently no cure for this infectious condition;nevertheless,there are efficient retroviral medications for improving patient health;yet,overuse of these drugs can have dangerous side effects.According to research,HIV infection is considered to be the most dangerous infection in the world affecting different sectors.HIV affected 1.8 million individuals in 2017,with 940 000 people dying from the illness.We believe that we can put a stop to the AIDS epidemic.Between 2010 and 2019,there was a 23% decline in new HIV infections worldwide.A larger number of people are receiving treatment than ever before.It is noticed that people may have symptoms that are similar to a sore throat,rash,headache,fever and influenza.Sometimes the symptoms are serious such as diarrhoea,fever,cough,weight and swollen lymph nodes.The infections develop serious conditions if the treatment is not serious.
Nowadays,modeling of natural phenomena is becoming a field of increased focus for researchers.Such models give sufficient information about the different dynamics of infectious diseases[1].Rashid and Xiao[2,3]studied the individual’s loss of immunity due to which they move to the susceptible class and they also evaluated the periodic transmission of dengue and seasonality in vectors.In 1999[4],the authors introduced an HIV model and indicated the most valuable control numerically.The authors in[5–7]developed different models to study the dynamics and key factors like viral mutation,intracellular delays,etc.The researchers in[8]incorporated two mechanisms such as infection by free virions and cell-to-cell direct transmission.The author in[9]examined the interaction through a model that consists of four different classes of population of HIV with CD4+T-cells.Perilson and Nelson in[10]have uncovered some important features with the help of a dynamical model by using a parameter estimation method.Raun and Calshaw[11]analyzed the model already presented by Perilson and Nelson in[10],and modified it into three different classes,where they considered free-virus,infected and healthy CD4+T-cells.Samia et al[12]conducted research and studied the phenomena of HIV-1 infection through fractional calculus.Ghoreishi et al[13]examined the HIV model by homotopy analysis method and also the researchers in[14–16]used a wide variety of ideas and techniques to analyze the dynamics of HIV.In[17],the chaotic phenomena of the dynamical system of HIV infection have been interrogated and analyzed.
Fractional differentiations are widely used due to their memory effect and they produce the best fit for the data of infectious disease as compared to the classic differentiation[18–21].The fractional derivatives outperform due to inherited properties and memory effect[22–25].Moreover,due to such features of fractional differentiation,these are used in modeling the phenomena of complex problems in various disciplines such as chemistry,physiology,technology,sociology,physics etc[26–28].Over the last decades,different definitions of fractional calculus have been utilized to model and investigate the transmission phenomena of different infections.In the literature,mostly biological phenomena are more precisely structured and modelled through fractional derivatives[29,30].The transmission phenomena of HIV have been conceptualized with preventive measures through the theory of optimal control[31].Furthermore,noninteger derivative possesses extraordinary characteristics which make it superior to integer derivatives.There are numerous operators in the literature on fractional theory,however,we choose Caputo and Atangana–Baleanu operators for the analysis of our model.The Caputo fractional derivative has the benefit of allowing standard boundary and initial value conditions to be incorporated in the problem formulation while the Atangana–Baleanu represent natural phenomena with nonlocal and non-singular.Therefore,we opt to present the dynamics of HIV infection through fractional calculus to understand the interaction of CD4+T-cells with HIV-free viruses in the body of the host to highlight the major aspects of the phenomena and to provide a good intervention with the health departments for the control of HIV infection.
In the second section of this research work,we constructed the transmission dynamics of HIV infection to show the interaction of CD4+T-cells and HIV viruses with control interventions.The hypothesized system of HIV infection is then presented through Caputo and Atangana–Baleanu fractional operators for more accurate outcomes.The basic results and theories of the proposed fractional system are listed in section three for the analysis of the HIV system.In section four,a numerical technique is introduced to highlight the solution pathways.The system’s most important parameter has been identified in section five of the research work through numerical simulations.
In this section of the work,we structured the transmission phenomena of HIV to visualise the interaction of healthy T-cells,infected T-cells and HIV-free viruses which are symbolized by T,I,and V,respectively.In the past,several researchers formulated the dynamics of HIV and tested it to study the complex phenomenon of HIV[32–34].They looked at numerous elements of HIV infections and discovered distinct input parameters for their models.The transmission phenomena of HIV were formulated by the researcher in[15]as follows
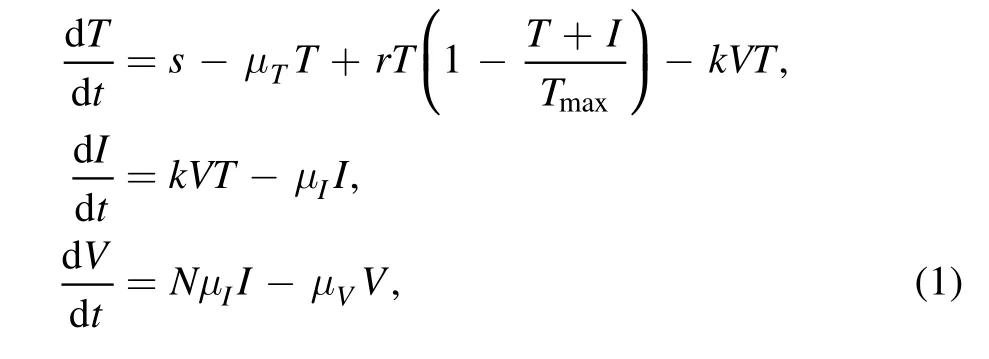
where s denotes the rate at which new T-cells are recruited into the body and μTdenotes the rate at which T-cells die while μVand μIindicate the death rate of HIV viruses and infected T-cells.The infection rate of healthy T-cells is indicated by k and N is the reproduction number of cells by infected T-cells.The Perelson and Nelson[35]HIV model with saturation incidence is given as
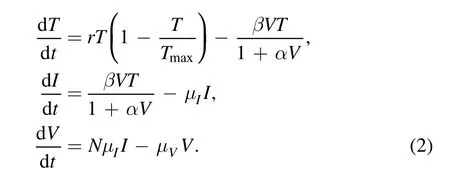
Here,we anticipated that healthy CD4+T-cells become infected by infected T-cells and HIV viruses via a saturated incidence rate.We also assumed variable termsexp(-κV)instead of a constant one.The wordsexp(V)represent the quantity of new healthy T lymphocytes generated via the thymus as a function of viral load concentration.Then according to[36],the system of HIV infection with variable source terms is given by
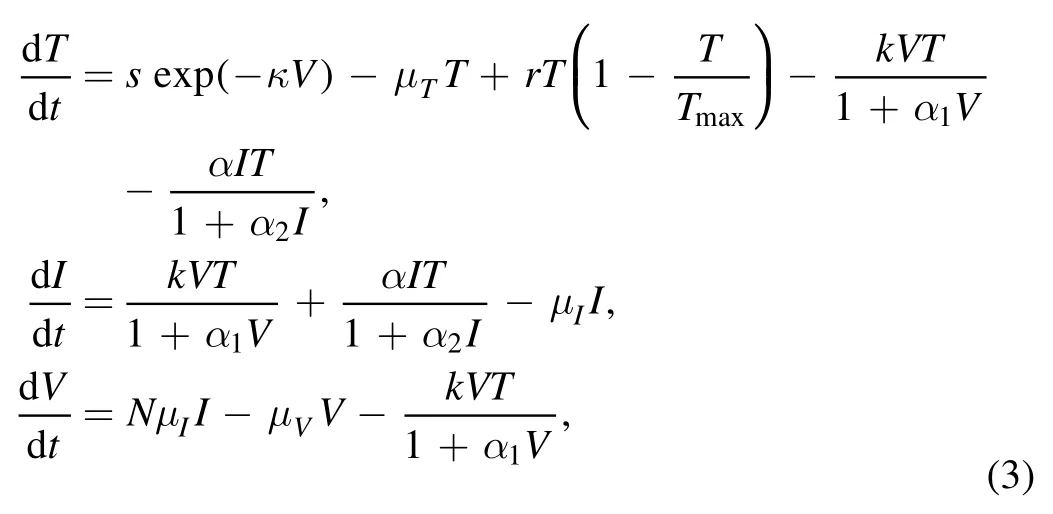
in which α is the efficiency of a protease inhibitor and is thecellular infection rate,respectively.Antiviral treatment is used to introduce three control measures.The aforementioned HIV infection dynamics with the control intervention become as

Table 1.Interpretation of input parameters and state-variables of the system with values.

In the above model,we introduce the control measures c1(t),c2(t)and c3(t).The function c1(t),c2(t)indicates the efficacy of drug therapy in blocking the infection of new cells,and the control indicates the efficacy of drug therapy in inhibiting the production of viruses,respectively.There is no blockage if c1(t)=0 and the blockage is 100 % effective if c1(t)=1.
Here,we recalled some basic concepts of Caputo and Atangana–Baleanu fractional operators for the analysis of HIV infection model.Firstly,we introduce the results of the Caputo operator which are given as follows:



Here,we will represent the new HIV infection model(4)in the framework of the Caputo derivative and will introduce a numerical technique for the Caputo operator to highlight the dynamics of HIV.The new model(4)of HIV in the Caputo framework is
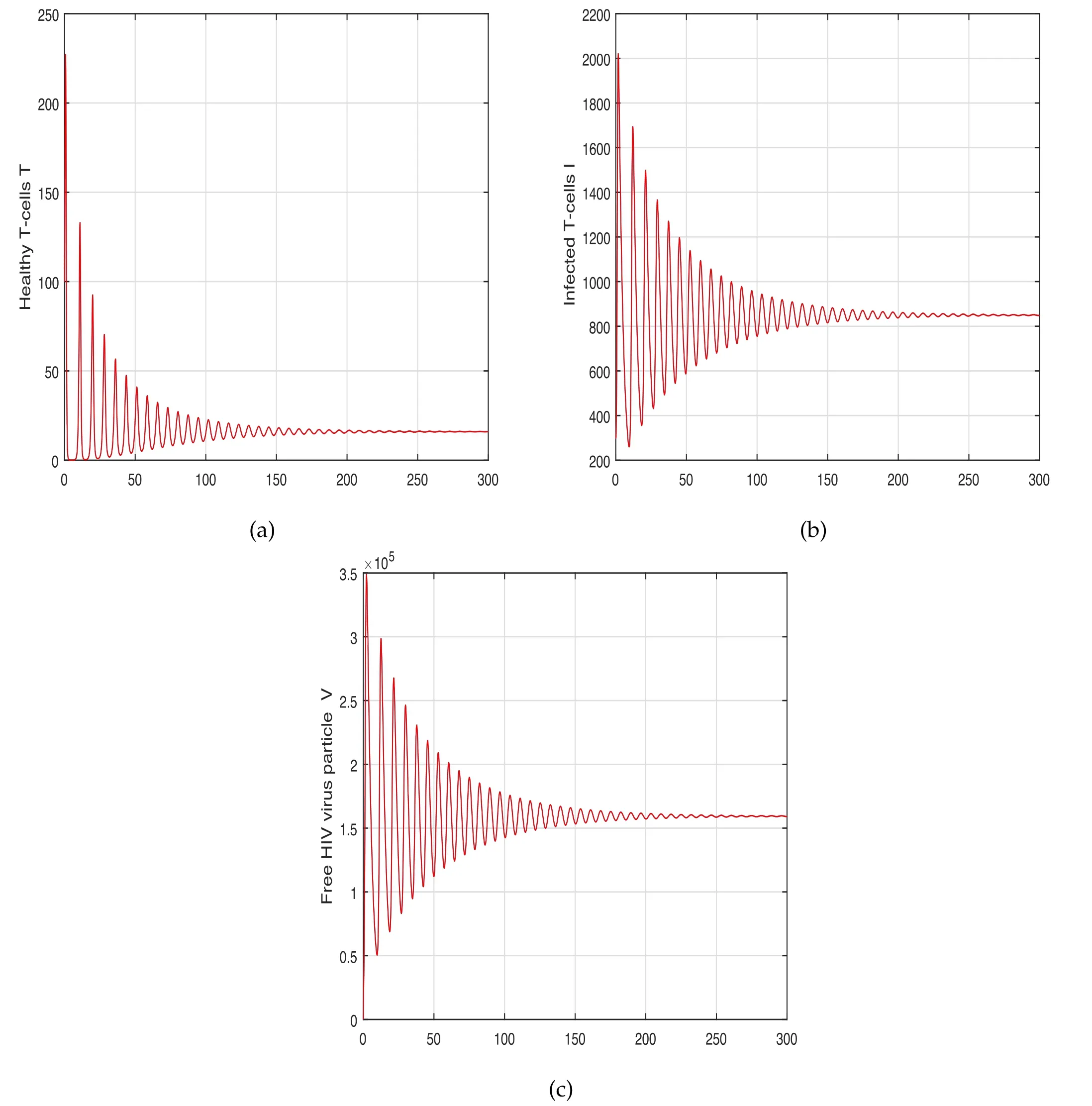
Figure 1.Graphical view analysis of the time series of the system(5)to conceptualize the dynamical behaviour of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses with input factor α=1.0.
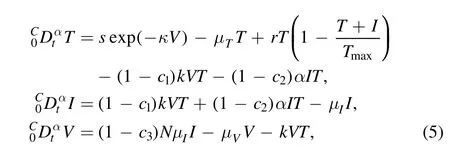
4.1.Numerical scheme for Caputo system
A numerical approach is presented for solving the fractional HIV model in the Caputo sense(5)is presented in this subsection.The current approach,which we utilise to solve the fractional Caputo nonlinear ordinary differential equation,is described in[37].The below steps are followed to obtain the scheme
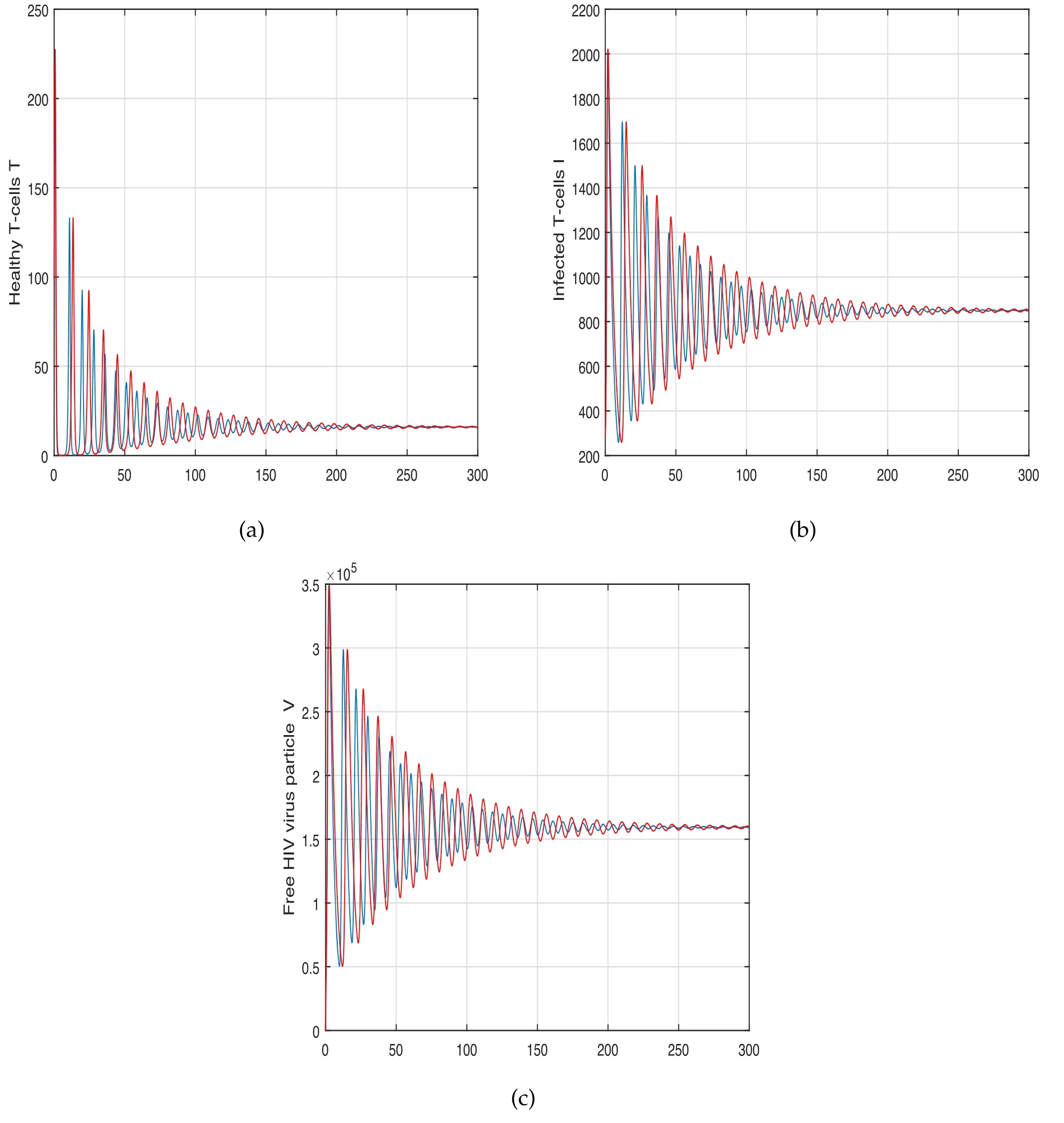
Figure 2.Graphical view analysis of the time series of the system(5)to conceptualize the dynamical behaviour of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses with input factor α=0.8.
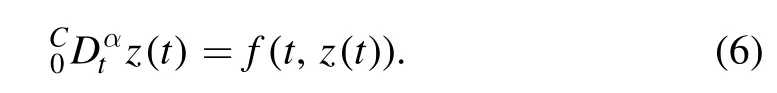
Applying the fundamental theorem,we have the following here,we take the time t=tn+1,n=0,1,…,and get
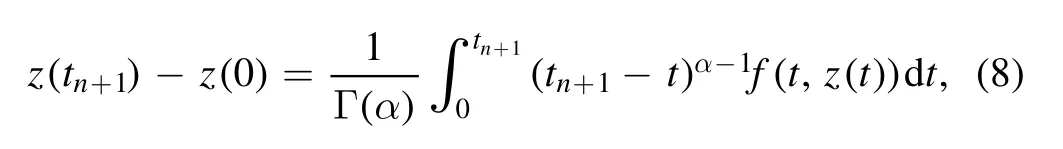
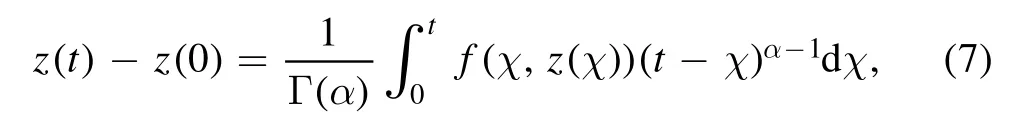
and
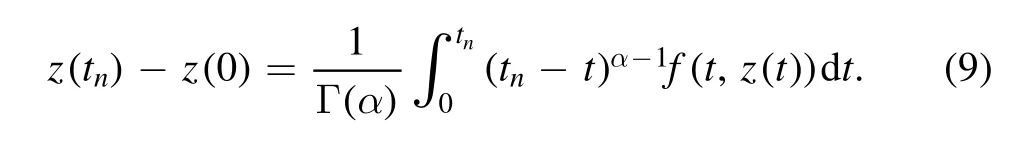
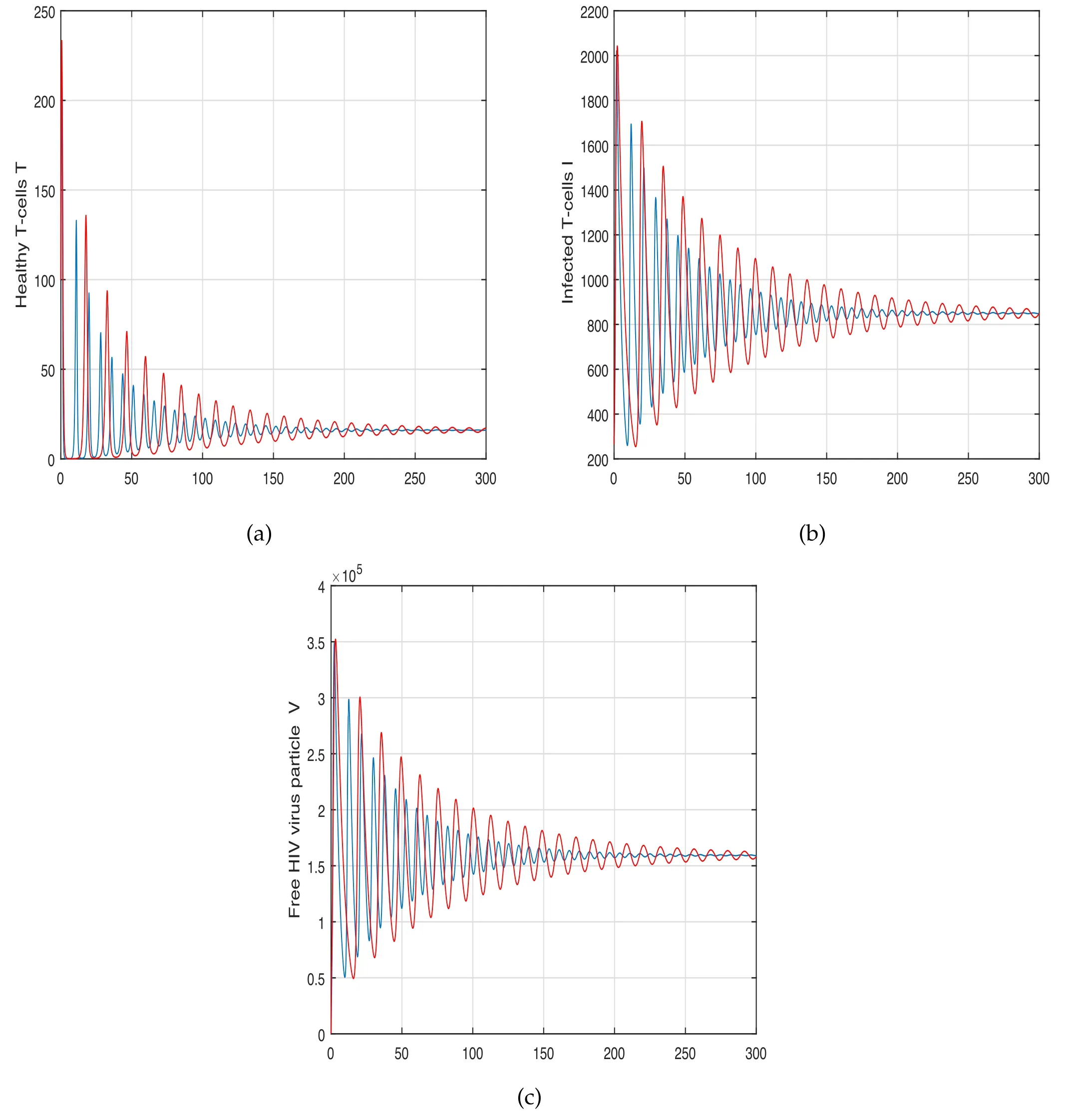
Figure 3.Graphical view analysis of the time series of the system(5)to conceptualize the dynamical behaviour of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses with input factor α=0.6.
Equations(9)and(8)imply that
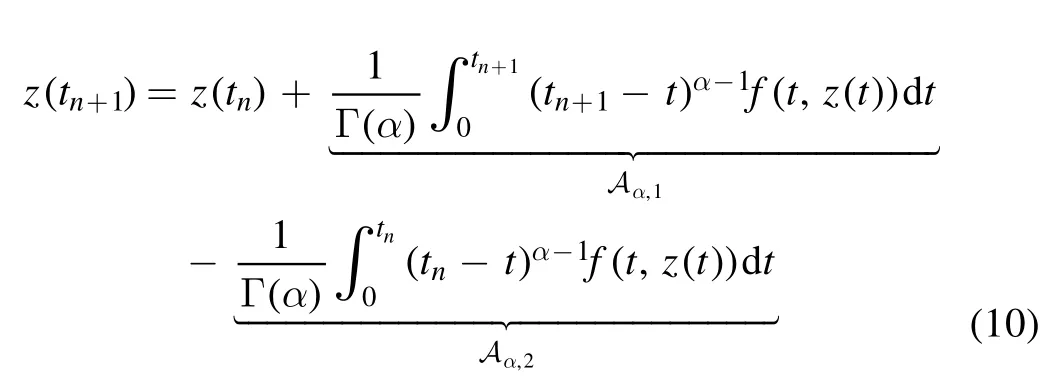
in which
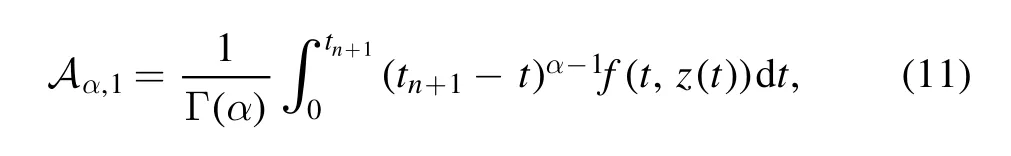
and
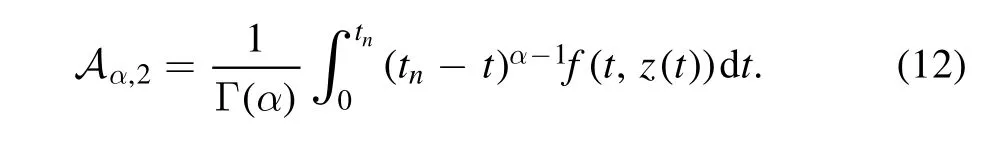
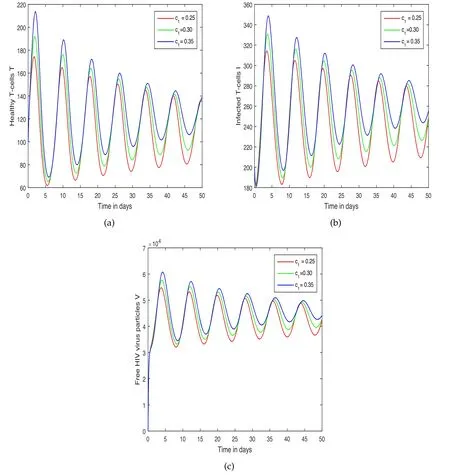
Figure 4.Representation of the dynamical behaviour of the system(5)to visualize the concentration of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses with different values of the control variable c1,i.e.c1=0.25,0.30,0.35.
Then f(t,z(t))is approximated in the below manner
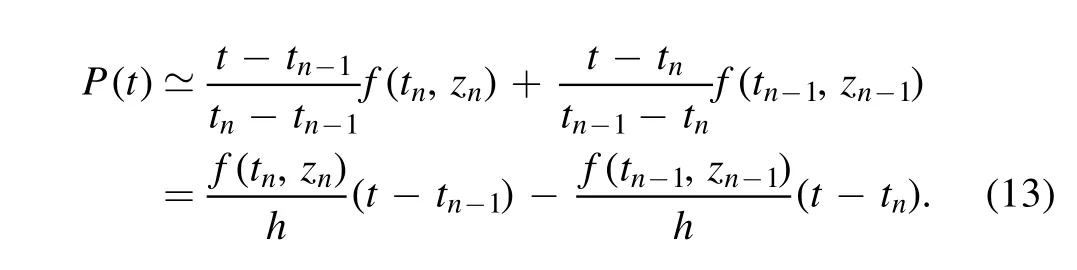
We get the following after simplification
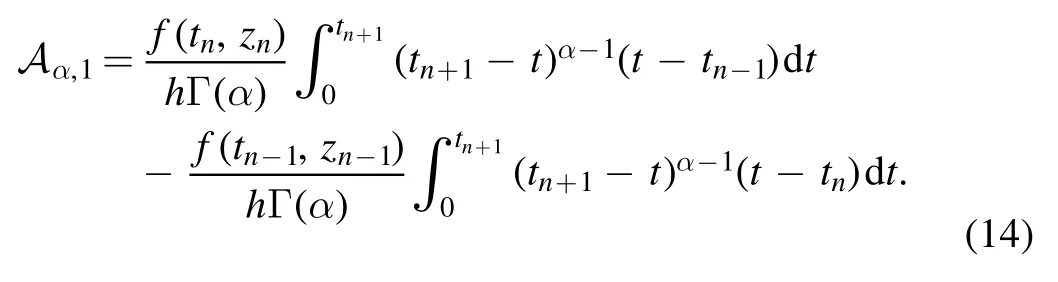
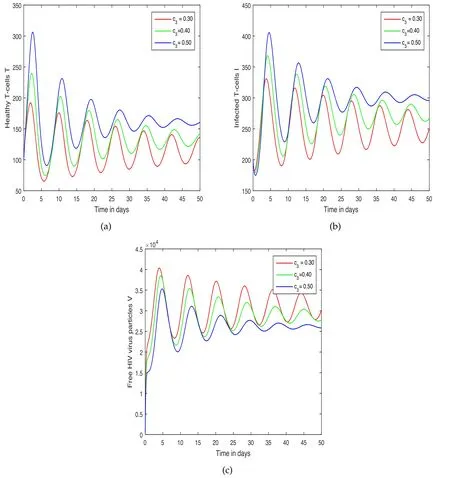
Figure 5.Representation of the dynamical behaviour of the system(5)to visualize the concentration of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses with different values of the control variable c3,i.e.c3=0.3,0.4,0.5.
Further,we have
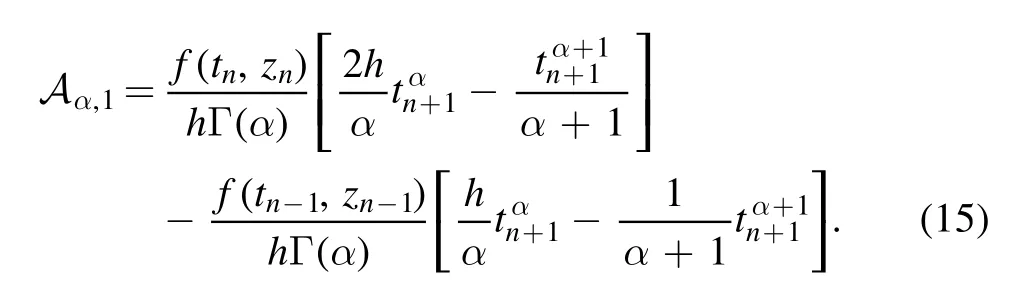
In the same way
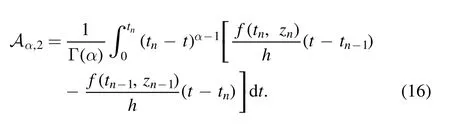
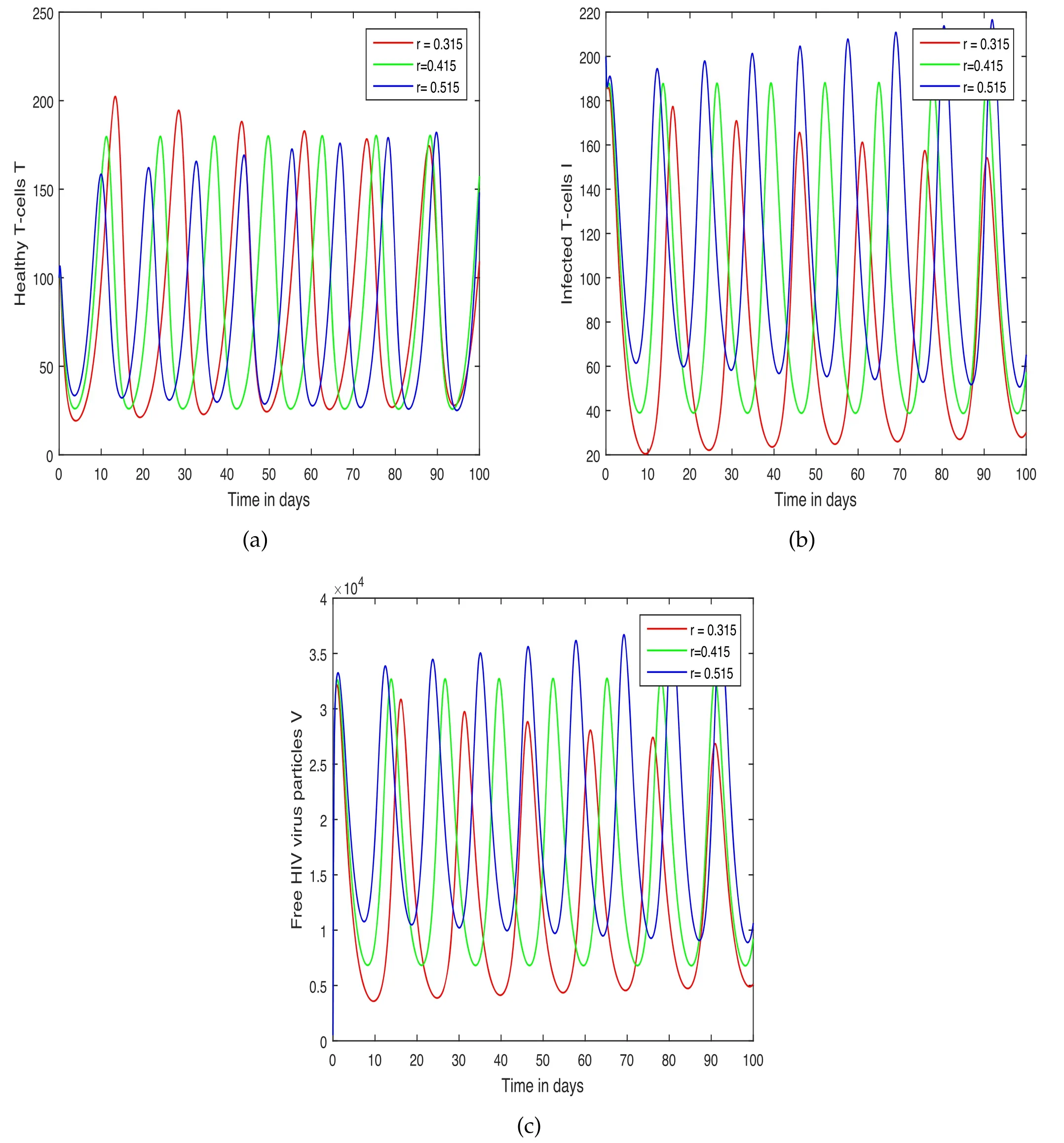
Figure 6.Effect of the input factor r on the concentration of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses of the system(5)of HIV infection.
Further simplifying,we get
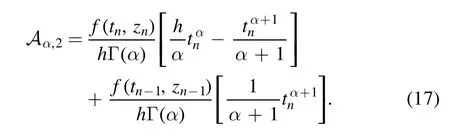
Putting equations(16)and(17)into(10),we obtained the following approximate solution
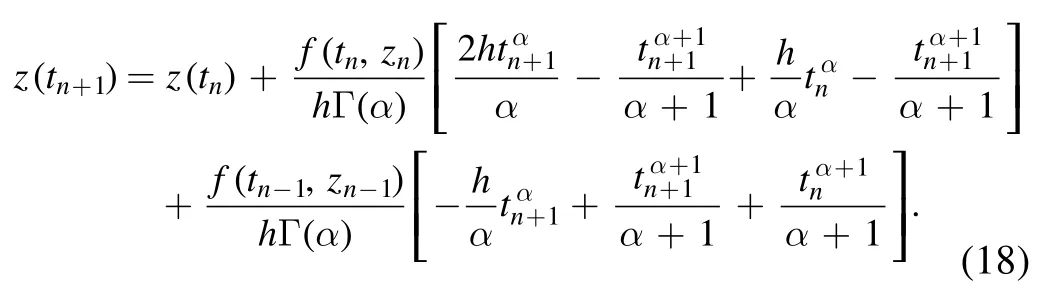
We represent the transmission phenomena of system(5)of HIV through this numerical scheme.The parameter values presented in table 1 are utilized for numerical purposes.
Here,we will represent the new HIV infection model(4)through the fractional derivative of Atangana–Baleanu.Then we will introduce a numerical technique for ABC derivative to visualize the contribution of several factors to the system of HIV.First,we represent our model(4)through Atangana–Baleanu derivative as

5.1.Iterative scheme with simulations
Here,we present a numerical approach for doing various simulations to demonstrate the influence of input parameters on the system’s output.We begin by rewriting our HIV infection system in integral form using the fundamental theorem of fractional calculus as



This numerical scheme is used to find out the solution to the ABC fractional system.We will utilize this scheme to investigate the transmission phenomena of the fractional system(19)of HIV infection.
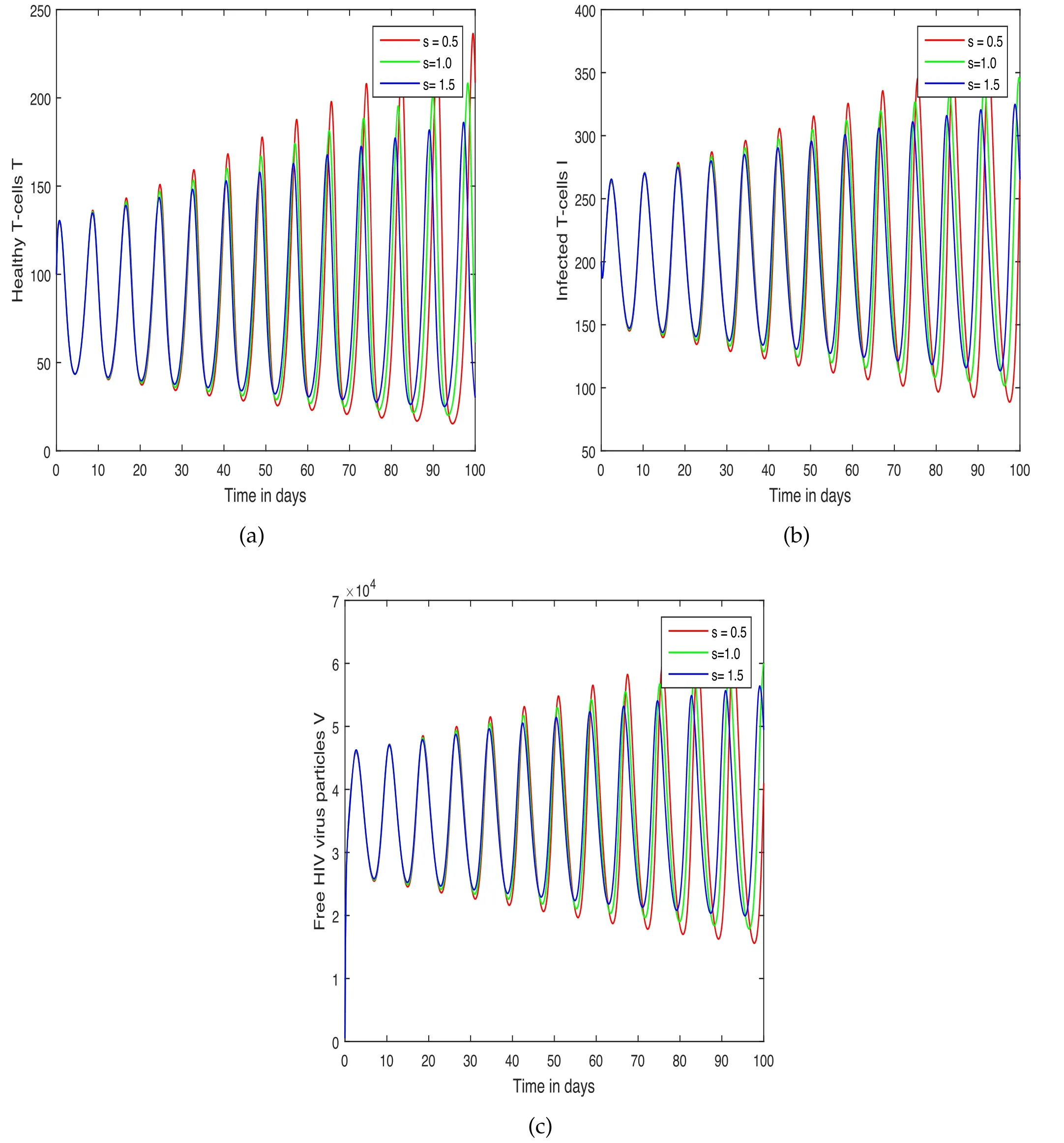
Figure 7.Effect of the input factor s on the concentration of(a)healthy T-cells,(b)infected T-cells and(c)HIV-free viruses of the system(5)of HIV infection.
Despite the tremendous worldwide efforts to combat HIV/AIDS,HIV/AIDS continues to be a significant burden for afflicted households in APR.This burden is exacerbated by decreased work income,higher healthcare spending,and a loss of capital to cover the income-to-expenditure gap.Hence,it is valuable to investigate the main factors of HIV infection for the control of these losses.The key purpose of this phase of the research is to visualise the system’s time series and chaotic behaviour in order to grasp the influence of various aspects on the system.To explore how the input factors impact the HIV dynamics,we employ a range of numerical scenarios.

Figure 8.Illustration of the dynamics of HIV infection to show the chaotic phenomena of(a)healthy T-cells,infected T-cells and HIV-free viruses,(b)health T-cells versus infected T-cells,(c)infected T-cells versus HIV-free viruses and(d)HIV-free viruses versus healthy T-cells with α=0.9,r=2.8 and s=1.0.
The system’s oscillatory behaviour has been depicted in the first scenario in figures 1–3 with various fractional order values.The fractional parameter has been found to have a significant influence on the system’s solution routes.The order of the fractional derivative has been discovered to have a favourable impact on HIV dynamics and might be utilized as a preventive measure.We exhibited the variance in control measures c1and c3in the second scenario shown in figures 4–5,while the impact of input parameters r and s were highlighted in figures 6 and 7,respectively.In the last scenario presented in figures 8 and 9,the chaotic phenomena of the system of HIV are obtained through fractional parameters.We displayed the chaotic behaviours of the system using various values of α.A comparative analysis of both the operators is presented numerically in figure 10 to illustrate the effect of these operators on the system.It has been noticed from these figures that the system exhibits a strong chaotic phenomenon and that the chaos may be controlled using these input parameters.Because of the nonlinearity of the suggested system,the oscillatory and chaotic nature of the system are inextricably intertwined.It has been revealed that this input parameter has a substantial impact on the system and that reducing the fractional order can lessen the number of HIV infections;as a result,policymakers are advised to use this parameter.
The theory of chaos is concerned with nonlinear phenomena that are difficult to anticipate or regulate.This phenomenon is primarily concerned with the deterministic principles and underlying patterns of the dynamical systems,which are extremely sensitive to initial values of state variables and were previously assumed to have wholly random states of chaos and irregularity.These circumstances are crucial because they reveal a lot about the system of HIV infection.Small perturbations can cause massive changes in the system,as seen by the chaotic behaviour of the system.These chaotic plots reflect the system’s instability and indicate how sensitive the system is to beginning circumstances,making it unpredictable.Our findings revealed that the system’s nonlinearity causes substantial oscillation and chaos,and that these behaviours are intimately coupled to one another.
HIV infection is known to attack the immune system and destroy T-cells,lowering the body’s ability to fight against other infections.It is currently a major public health concern across the world.Although new data shows that HIV infection is on the decline,additional research is needed to fully comprehend how HIV interacts with T-cells.Here,we structured the dynamics of HIV in order to analyse the transmission route of HIV infection.In our model,we imagined the interaction of HIV viruses,uninfected T-cells,and infected T-cells.The suggested system of HIV is then presented via Caputo and Atangana–Baleanu fractional operators.A numerical approach is presented and utilized to highlight the solution paths and chaotic behaviour of HIV infection.Various simulations have been carried out in order to depict the system’s most crucial situation.We have shown how the suggested system behaves in a chaotic manner.The effect of fractional-order on the HIV infection system’s solution routes has been demonstrated.The transmission process of HIV was highlighted by varying various input parameters for infection management and prevention.We discovered that chaotic and oscillatory behaviour are very closely connected.We will examine our HIV infection model in the future to see how medicine influences the virus’s path and come up with better cure plans.We will improve the model by incorporating delay into the system to show how delay influences HIV dynamics.The model will also be updated to incorporate vaccines and medications to show the impact of vaccination and treatment on the system.